



A design method for thickeners and clarifiers known as the batch flux curve technique was developed over 20 years ago, but still is not well-known in design and operating circles. An informal survey of major clarifier and thickener manufacturers found that none of the firms surveyed use this method for sizing and maximizing operating conditions. Here, we will show the benefits of using this technique, while illustrating it with an example from an actual plant design. The theory and applications will also be covered.
Clarifiers and thickeners are separation devices. They are common in waste treatment operations as well as in other chemical operations. These devices separate two phases by differences in their density. Clarifiers and thickeners are essentially ide ntical units; a clarifier produces clean water, while a thickener concentrates a solids slurry as the desired product.
In this discussion, thickener will be used to describe both units. Also, a gravity separation of solids from water is assumed to take place. The most common unit is a circular thickener.
The mass (Eq. 1) and material balances (Eq. 2) that form the foundation for the technique (see Figure 1) are:
Qf = Qu + Qe (1) Qf xf = Qu xU + Qe xe (2)
Under normal conditions, no solids are desired in the effluent:
xe = 0 (3)
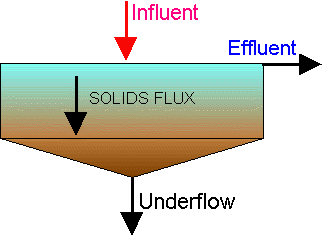
The feed flowrate (Qf) and concentration (xf) are normally design parameters. This leaves the designer or operator to determine the underflow pumping rate (Qu) (sometimes called blowdown) required to achieve a desired underflow effluent concentration (xu) . Since the underflow is normally pumped, this variable can be controlled during operation. Also, the pump must be sized to adequately handle the largest expected loadings.
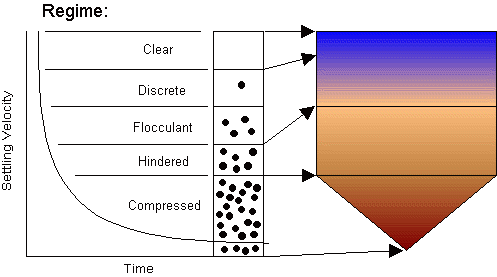
Four regimes of settling are recognized (see Figure 2):
Discrete settling occurs when particles are independent of each other, with no interparticle forces. Examples of this regime are removing sand and sub stones from water. In this regime a force balance using Stokes' law is appropriate.
In flocculent settling the particles begin to influence each other, occasionally sticking together to form flocs. Design in the flocculent regime may use quiescent settling tests, or batch-flux design to improve the slurry product.
In hindered settling, particles are so close they have a major effect on each other. This is the regime in which batch-flux analysis applies.
The compression regime is not well studied, and since it normally operates only at the very bottom cone of the thickener, it goes beyond conventional design requirements.
The development of the technique began with Kynch, who modeled the settling of particles in water. This was followed by work of Yoshioka and Dick, and Ewing, which formed the current technique. Since the surface area of the settling unit is the main variable, the mass flow through the system is considered a flux, mass per unit area per time. This allows system properties to be described in a general way for any size unit.
In summary, the technique looks at steady-state conditions as solids move downward in a thickener at a single flux rate. The settling rate is a function of the feed solids concentration. This settling flux is combined with the flux caused by Qu< drawing product off the bottom, and balanced with the water rising out of the thickener. If the flux in (xf Qf/A) exceeds the flux out (xu Qu /A), solids will be carried out in the effluent.
In the batch flux method, a graphical technique represents the settling flux and the underflow flux as functions of solids concentration. The settling properties are plotted as a curve.
The applied flux and underflow pumping rate are presented as an operating line. The applied flux is the y-intercept of the operating line, and the pumping rate is the slope of the operating line. Determining the settling properties is more involved, and we will detail the experimental method and calculations required for generating the curve and applying it.
In settling, cross-sectional surface area is the key parameter. The depth of the tank is not a factor. The depths used in practice are typically 2.5 to 5 m (8 to 15 ft), which allow for inlet and outlet turbulence, and solids storage in the bottom of the unit. This dependence on area holds for discrete settling when Stokes' law applies, as well as for hindered settling, when the batch flux analysis applies.
The typical design procedure will be shown using data from a large industrial wastewater treatment facility, involving acid and base neutralization and heavy metals removal.
The objective is to determine the area of a thickener, the optimum underflow pumping rate, and the corresponding underflow concentration. The following data were taken: Qf = 177,600 kg/h; xf = 5 kg/m3; and [density], p f =1,000 kg/m3.

A = horizontal surface area, m2
G = solids flux, kg/m2/h
Q = flow rate, kg/hr [note]
r = radius, m
V = unhindered settling velocity, m/h
x = concentration, kg/m3
Subscripts
e = effluent
f = feed
i = test number (1 - n)
u = underflow
Greek letter
p = density, kg/m3
[note] mass and volume flows are used interchangably in this paper, you must use the slurry density to assure dimensional consistency.
Calculation of the curve requires several settling tests of thickener feed at various concentrations. The goal is to measure the unhindered settling velocity at several concentrations. Each test (i) produces a settling velocity (Vi) and a solids concentration (xi).
One large sample can be diluted or concentrated to make several samples of different concentrations. In diluting, use the supernatant as a dilutant rather than adding water. This keeps the solution chemistry consistent.
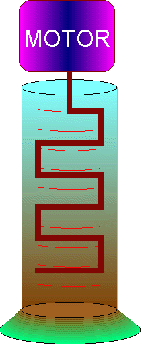
The test apparatus is simply a graduated cylinder or long glass tube, and a stopwatch. A wire stirrer operating at one rpm is required for slow settling materials such as bioprocess solutions to minimize wall effects (see Figure 3).
Condition the sample with flocculant, if required, at the recommended dosage rate. Mix the solution thoroughly, and then begin timing. The solid-solution interface is measured and recorded over time. Figure 4 shows the settling curve obtained for on e solids concentration. In testing, read the interface position on the mL graduations of the graduated cylinder. Then measure the graduations and convert the mL readings to length.
Test # tss (kg/mm3) v (m/hr) --------------------------------- 1 3.1 6.045 2 3.3 2.560 3 5.3 4.534 4 19 1.100 5 24 0.897 6 31 0.944 7 38 0.382 8 41 0.248 9 51 0.326 10 52 0.177 11 53 0.239 12 53 0.217 13 70 0.293 14 73 0.227 15 80 0.284 16 81 0.210 17 96 0.183 18 110 0.107 19 110 0.034 20 120 0.110 21 140 0.018 Table 1 Actual Settling Data
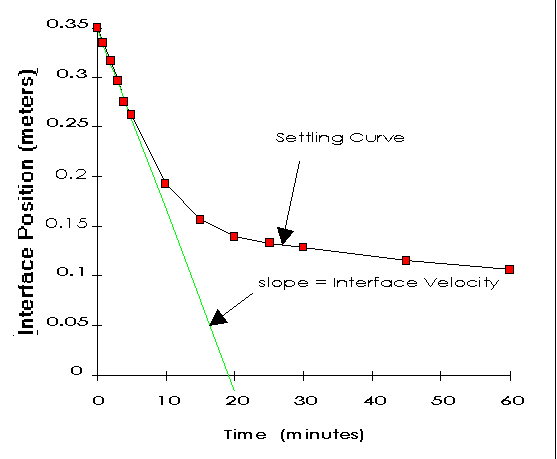
The straight line shows the estimate of the unhindered settling velocity. This can be calculated from the x and y intercepts:
(0.35 m/19 min) (60 min/1 h)
= 1.1 m/h (4)
Each solution is also analyzed for solids concentration. Normally total suspended solids (TSS) is used, but other measures, such as volatile suspended solids (VSS) for bioprocess work can be used. Table I shows the results for 21 different tests.
Often the velocity and concentration can be fit to a straight line on semilog coordinates (see Figure 5). The transformed data are represented by:
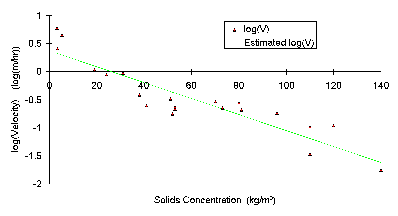
log V = m x + b (5a) or solved for V: V = 10(m x + b) (5b)
where m and b are the slope and intercept of the linearized data, respectively. In this case the values were estimated to be m = -0.0142 and b 0.370.
Use the fitted data for (xi, Vi,) to calculate the settling flux curve:
Flux = Gi = Xi Vi (6a) Illustrating at xi = 20 kg/m3: V20 = 10 ((-O.0142)(20) + 0.37) = 1.26 m/h (6b)
G20 = (20 kg/m3)(1.26 m/h) = 25.2 kg/m2/h (6c)
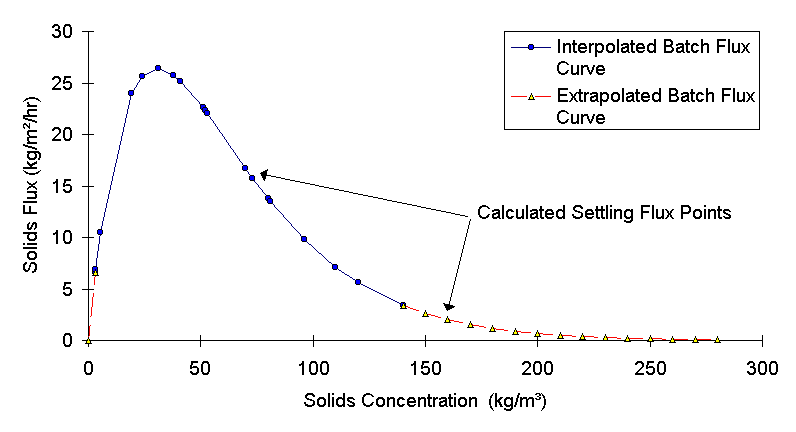
Calculate Gi for xi from 0 to 300 kg/m3 in intervals of 10, then graph as shown in Figure 6. In this example, estimates were calculated for experimental points outside the experimental range. The feed rate solids flux shown is calculated in the next step.
The applied solids feed rate can now be calculated as a flux - see Eqs. 8a and 8b.
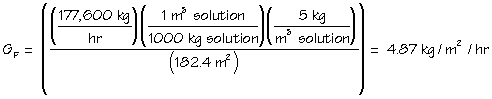 (8b)
(8b)Once the settling flux curve is drawn, the optimum operating point can be determined. To calculate the removal rate, construct an operating line from the feed point, tangent to the settling curve, and crossing the x axis. The x-intercept is the maxim um underflow solids concentration possible, as shown in Figure 7.
The condition described by this operating line is referred to as a critically loaded thickener. At steady-state the unit will provide optimum performance under these conditions.
The maximum thickened concentration in this example is 232 kg/m3. This is very concentrated for waste treatment applications. Typical thickened concentrations of biological treatment sludges are 5-15 kg/m3.
To find the corresponding pumping rate, solve Eqs. 2 and 3 for Qu. Since xe = 0, then -see Eqs 9a and 9b.
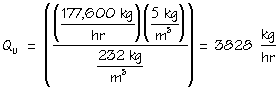 (9b)
(9b)Since these numbers are reasonable, an about 15 m (50 ft) diameter unit would work well. If the numbers were not reasonable, a new operating line could be drawn by inspection, and the area (A) and underflow (or withdrawal) rate (Qu) could b e determined for those conditions.
Qu is the steady-state sludge withdrawal rate. Keep in mind that the maximum flow requirement may be several times that depending on design, operation, and control scheme. A typical installation pumps the solids out once an hour using a ti med control.
The theory says to expect four concentrations in the unit at steady-state' as illustrated in Figure 8:
0 kg/m3 TSS (at the top);
5 kg/m3 TSS (the "thin blanket");
193 kg/m3 TSS (the "thick blanket"); and
232 kg/m3 TSS in the exit stream.
The layers of solids will move vertically to absorb variations in incoming flow and underflow pumping. Once the batch flux curve is constructed it can be applied in a variety of ways.
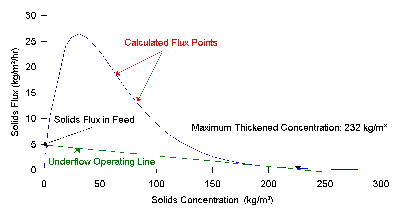
In practice, clarifier sizing is often based on a handbook value for a particular type of waste. Now, we shall compare a handbook value to the batch flux curve technique. These values are often reported as a rise rate. For this application 33-41 m 3/day/m2 (800-1,000 gal/day/ft2) is considered typical; the range for typical overflow rates is 16-73 (400-1,800) in the same units (1). The overflow rate in the previous batch flux curve illustration is:
Rise rate = wastewater flow rate/clarifier area = 23.4 m3/day/m2 (570 gal/day/ft2). Batch flux sizing of the clarifier has placed the size in the conservative end of the published design range.
Besides providing the security of smooth operation from an effluent standpoint, using the batch flux technique to size clarifiers also ensures control of the underflow. The achievable underflow concentration is easily calculated. For chemical process es, the batch flux technique can be applied to new systems that lack published guidelines. The size calculated can be compared to published clarifier ranges to check for reasonableness.
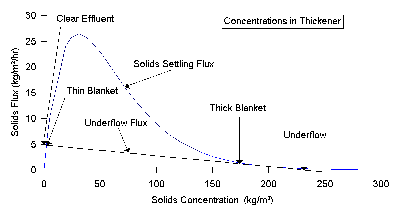
The major benefit of the batch flux curve is during operation. The curve plots the solids loading and expected underflow concentration, and determines the required pumping rate to achieve the greatest separation from the equipment. The idea is to ach ieve a critically loaded settling unit. This is done by constructing operating lines as illustrated in the thickener design example.
Figure 9 and Table 2 illustrate the effects of underloading, critically loading, and overloading a thickener.
Underloading is the most common condition found in a thickener (see Figure 9). In this case, the sludge blanket is not allowed to develop, and excess water is pumped out of the thickener underflow. Figure 9 shows an underflow of only 150 kg/m3 of TSS. (This is the same unit as just calculated, but run at a different underflow concentration.)
Using Eq. 9a the current pumping rate would be - see Eq. 10.
In this case, the new operating line would be constructed to determine the optimum underflow concentration. Use the design procedure to determine the optimum underflow concentration and calculate the flow required to reach it. Since the new pumping r
ate will be lower, there will be energy savings as well as improved operation. The product concentration will change from 150 to 232 kg/m3; and the pumping rate from 5,920 to 3,830 kg/h, at critically loaded flow.
Overloading causes the operating line to cross the curve at 140 kg/m3. This is the exit concentration, xu. Use the slope of the operating line to calculate the underflow rate: - see Equation I 1.
If operated this way for long, solids will accumulate and rise to the overflow, contaminating the effluent. Eqs. 2 and 9a can be used to calculate the effluent concentration (xe). - see Equation 12.
This shows the effect of overloading a thickener by pumping too little underflow.
Other operational problems can occur, such as intermittent overloading and varying sludge properties. In each case, the batch flux curve is determined for each material and the operating line is constructed.
Problems can also arise with improper dosing of flocculent. Often, an underdose can drastically change the settling properties. This points out the importance of properly conditioning the samples with flocculent before each batch settling test.
For biological treatment processes, an important extension of the batch flux curve is the state point (see Figure 10). Developed by Keinath, et al. (2), the state point adds operating lines for reactor recycle, allowing the thickener operation to be a
djusted to optimize the entire system. The state point operating line crosses the batch flux curve operating line at xr, the concentration of cells in the reactor.
This concept is useful in operating many kinds of biological reactors. In Figure 11, by pumping the clarifier at a lower rate to achieve critically loaded operation, the cell concentration in the reactor will increase giving better treatment. This co
ncept can be extended to inorganic treatment by substituting the crystal growth equation for the cell growth equation.
Another use is for thickeners in series, using the recycle from the second stage as part of the makeup to the first stage (3). Using sequential thickening steps, deliberate overloading of all but the last step may give distinct advantages.
Using thickeners in series is good for slow settling materials. This setup is thought to take advantage of the compressive settling regime for consolidation of thickened solids. A polishing unit provides a clear effluent. This technique allows more
control over the finished product, and allows equipment sizing to be optimized for the lowest-cost thickened product.
A third important concept is inorganic solids recycle. This technique is useful in treating heavy metals and other ionic species in solution. By recycling solids and mixing them with the feed material, greater removal is often achieved (4).
This technique employs several mechanisms, including providing seed crystals, decreasing precipitate surface tension, raising the ionic activity, providing an ion-exchange site, and ultimately decreasing the solubility allowing more ions to be removed
from solution, yielding a cleaner effluent. The batch flux curve and state point can be used to determine the mass balance in solids recycle system, allowing steady-state process conditions to be optimized.
[CEP]
Page 11, October 1994 CEP In Table I of the July article, "improve Clarifier and Thickener Design and Operation," by Joel Christian (pp. 50-56), the titles Vi and TSS are reversed. The first TSS is 3.1 and the first Vi is 6.045. In the overloaded case on p. 55, the underflow c
oncentration should be 240 kg/m3, not 140. Also, the dashed line in Figure 9 is not used in the calculation. The actual operating line would be parallel to that and tangent to the curve, showing the portion of the feed flux actually removed i
n the underflow. These corrections have been made in this HTML version. This article also appears in the Encyclopedia of Chemical
Processing and Design, J.J. McKetta, Editor, Marcel Dekker
Inc., Volume 58 p61-77 (1996).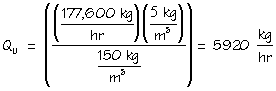 (10)
(10)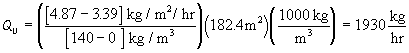 (11)
(11)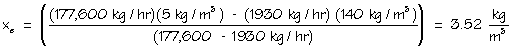 (12)
(12)
Figure 9. Effects of underloading and overloading.
Advanced applications


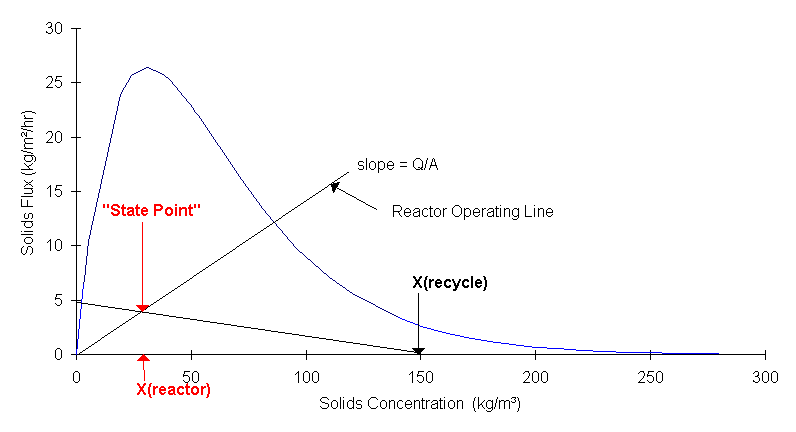
Figure 10. State point for a biological reactor and clarifier.

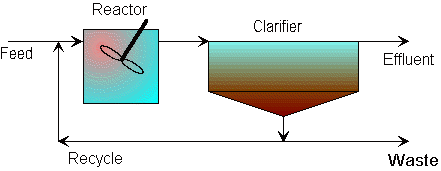
Figure 11. Typical bioreactor and clarifier setup.


Literature Cited

Further Reading

Corrections
Click here to e-mail comments and suggestions to the author, joel@joelbchristian.com.