Combine Fault and Event Trees for Safety Analysis

CHEMICAL ENGINEERING PROGRESS

April 1997 pp. 72-75

Reprinted with permission from Chemical Engineering Progress, April 1997. Copyright � 1997 American Institute of Chemical Engineers. All Rights Reserved. Not to be uploaded to any other site without written permission from the AIChE. Individual downloads are permitted so long as a fee of $15 per article is paid directly to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923.

Joel B. Christian, OSRAM SYLVANIA INC.

[BAR]

These combined trees yield the probability of each consequence. By diagramming the failure logic and computing each branch, overall system reliability can be determined.
[BAR]

Process engineers are often asked to evaluate the reliability of a piece of equipment or a process. The evaluation may be for quality reasons, reliability, preventative maintenance, or, more often, to evaluate process safety. Quantitative reliability methods are proven tools for predicting system reliability and quantifying potential outcomes. These methods help us to make better decisions regarding the use of public and private resources. Such methods are applied daily in government and public welfare, as well as in industries such as insurance, finance, and the chemical process industries (CPI).

Decision trees can be combined with utility functions (1) to make an overall determination of the risks and value of different alternatives in a system. In this article, we will look at applying fault and event trees as tools to predict process safety. As an example, we will look at a hypothetical heat-treating chamber where any oxygen present could produce an explosive atmosphere. The probabilities are expressed as the probability of an event during any one-hour period. The probability P of an event is a number from 0 to 1. Individual events in a sequence have a probability of E and a reliability of (I - E) = E.

Fault trees trace the path of various faults in a system. Figure I shows such a figure for the loss of purge gas in the heat-treating chamber.

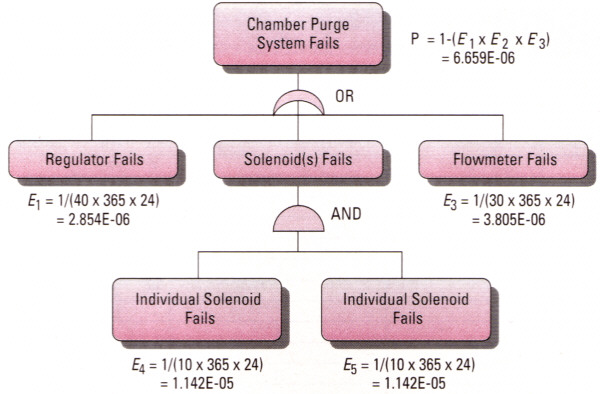
Image of Figure 1

Figure 1. Fault tree for the loss of purge gas in the heat-treating chamber.

Event trees show the potential course based on an initial event. Fig- ure 2 is the event tree of outcomes for the loss of purge gas.

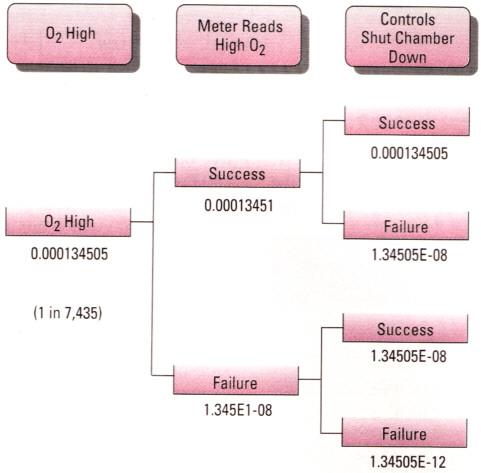
Image of Figure 2

Figure 2. The event tree of outcomes for the loss of purge gas.

Combining fault and event trees

Newer matrix techniques allow any combination of faults and events to be computed as an overall system, and provide an excellent quantitative tool. For simpler problems requiring a clear presentation to people of varied backgrounds, combine the fault tree and event tree, joined at a common critical event. Using this technique presents a logical list of failures linked to a list of possible outcomes. Once probabilities are assigned to each branch, the overall reliability can be determined, as shown in Figure 3. When working with reliability, we treat individual probabilities as if they were absolute. We may be basing the number on years of historical data, combined data, data from similar systems, or even a guess. Once the system is defined, it can be refined to give a truer picture of the actual process. Remember, the reliability model you construct is only as true-to-life as you can make it�if you omit a scenario or guess at outcomes, the over all estimate will be less accurate.

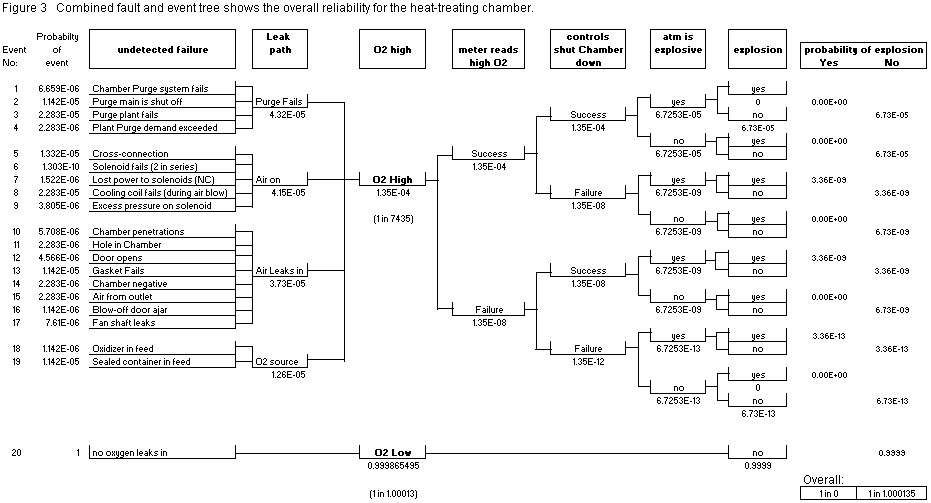
Image of Figure 3 (large)

Figure 3. Combined fault and event tree shows the overall reliability for the heat-treating chamber.

The tree elements are computed using Bayes' theorem, which was proposed by Thomas Bayes in about 1760. This theorem allows us to compute conditional probabilities for sequences of events. The branches of the tree are treated as reliabilities E' rather than failures E. Thus, if the probability of a failure is 0.001, the reliability is (1 - P), or 0.999.

Each branch of the tree connects at a logic point describing the physical system with a logical AND or a logical OR gate. With a logical AND, the combined probability P is equal to (E₁ x E₂ x E₃). With a OR, the combined probability is equal to 1 - (E'₁ x E'₂ x E'₃). Combining the branches along the tree, the probability of each consequence can be computed. By diagramming the failure logic and computing each branch, the overall system reliability can be determined.

Combining a fault and event tree can be useful in quantifying and visualizing potential hazards. Various root causes can be traced through the tree to the branch bearing the outcome. Figure 3, as noted before, illustrates the combined system for the explosion hazard due to the loss of purge gas. The results are summarized in Table 1.

Table 1. Predicted outcomes for the explosion hazards in the heat-treating chamber.

Event	Probability	Odds
Normal Operation	9.999E-01	1 in 1.000135
Oxygen High (alone)	1.345E-04	1 in 7,435
Oxygen High with no explosion	1.345E-04	1 in 7,434
Oxygen High with explosion	6.726E-09	1 in 148,685,875

A major challenge in quantitative risk analysis is in finding representative data. AIChE's Center for Chemical Process Safety (CCPS) has published several references (see "Further Reading") which are an excellent starting point for obtaining probabilities for various types of events.

Finally, the combined fault and event tree can be extended beyond process safety analysis to aid in decision making for various business decisions, marketing plans, and public policy decisions, where one or more varied conditions might lead to many different outcomes through one or two main channels.

CEP

Literature Cited
(1) Christian, J.B., "Use Utility Functions to Select Capital Equipment," Chemical Engineering Progress 91(3), p.92 (March 1995).

Further Reading
Center for Chemical Process Safety, "Guidelines for Chemical Process Quantitative Risk Analysis," CCPS, AIChE, New York (1989).
Center for Chemical Process Safety, "Guidelines for Preventing Human Error in Process Safety," CCPS, AIChE, New York (1994).
Covello, V.T., "Decision Analysis and Risk Management Decision-Making: Issues and Methods," Risk Analysis, 7 p.131 (1987).
Keeney, R.L., "An Analysis of the Portfolio of Sites to Characterize for Selecting a Nuclear Repository," Risk Analysis, 7 pp 195-218 (1987).
Greenberg, H.R., and J.J. Cramer, "Risk Assessment and Risk Management for the Chemical Process Industry," Van Nostrand Reinhold, New York. (1991).
Moore, P.G., and H. Thomas, "The Anatomy of Decisions," Penguin Books, (1976).

J. B. Christian is an Advanced Research Engineer at OSRAM SYLVANIA INC., Towanda, PA (570-268-5345; Fax: 570-268-5350; e-mail: christian@cornell.edu). He has 15 years experience in project management, chemical and environmental process design, operation, and management. He holds a BSChE from SUNY at Buffalo and a M.Eng. (Chemical) from Cornell University. He is a diplomate of the American Academy of Environmental Engineers, and a Registered Professional Engineer in New York and Pennsylvania.

Back to author's homepage